[계산이론] #03. Regular Expression

저번 글에서 3가지 Regular Operation, Union, Concatenation, Star에 대해 알아보았는데요, 이번 글에서 다룰 Regular Expression에 대해 본격적으로 알아보기 전, 또 다른 Regular Operation들에 대해 간단히 알아봅시다.

 

Complement & Intersection

Alphabet $\Sigma$에 대한 Lanauge $A$에 대해서, $A$의 Complement $\bar{A}$는 아래와 같이 정의할 수 있습니다.

$$\bar{A}=\left\{w\in \Sigma^{*}:w\notin A \right\}$$

이때, $A$가 Regular Language라면 $\bar{A}$ 역시 Regular Language입니다. 이는 Complement 역시 Regular Operation임을 의미합니다.

그리고, 두 집합의 교집합을 나타내는 기호 $\cup$ 역시 Regular Operation입니다. 즉, $A$와 $B$가 Regular Language이면, $A \cup B$ 역시 Regular Language입니다.

 

Regular Expression이란?

저희가 어떤 문자열의 집합, Language를 설명할 때, 보통 우리는 이 집합에 속한 문자열들의 특징을 나열해서 이 집합을 설명합니다. 예를 들어 아래와 같은 집합이 있다고 생각합시다.

$$A=\left\{ 0, 01, 011, 0111, 01111,\cdots, 1, 11, 111, 1111, \cdots \right\} $$

이 집합을 말로 풀어보면, "0 혹은 1 뒤에 음이 아닌 정수개의 1이 붙은 Binary String의 집합"이 됩니다. 이렇게 말로 집합에 대해 설명할 수도 있지만, 이때까지 배웠었던 Regular Operation을 이용해 아주 간단하게 나타낼 수 있습니다.

$$\left ( 0 \cup 1 \right )1^{*}$$

아마 Regular Operation을 다 알고 계시다면 대충 감이 잡힐 것입니다. $\left ( 0 \cup 1 \right )$는 $\left\{0, 1 \right\}$을 의미하고, $1^{*}$은 $\left\{\epsilon ,1, 11, 111, 1111, \cdots \right\}$를 의미하므로, 이 두 개를 붙여놓으면 $A$ 집합과 완전히 일치함을 알 수 있습니다.

이렇게 Alphabet과 Regular Operation을 활용하여 Language를 나타내는 것을 Regular Expression이라고 합니다.

 

Regular Expression의 예시

여러 가지 예시를 보면서 이해를 좀 더 해봅시다. 0을 정확히 2개 포함하는 Language는 아래와 같은 Regular Expression으로 표현 가능합니다.

$$1^{*}01^{*}01^{*}$$

"1011"을 포함하는 Language는 아래와 같이 표현 가능합니다.

$$\left(0\cup 1 \right)^{*}1011\left ( 0\cup 1 \right )^{*}$$

길이가 짝수인 Language는 아래와 같이 표현 가능합니다.

$$\left ( \left ( 0\cup 1 \right )\left ( 0\cup 1 \right ) \right )^{*}$$

처음과 마지막이 같은 Language는 아래와 같이 표현 가능합니다.

$$0\left ( 0\cup 1 \right )^{*}0\cup 1\left ( 0\cup 1 \right )^{*}1\cup 0 \cup 1$$

아마 읽어보시면 이해가 다 될 정도로 간단한 내용이라 추가적으로 설명은 하지 않겠습니다.

 

Regular Expression의 수학적 정의

이제 Regular Expression이 무엇인지 감은 다 잡으셨을 겁니다. 이제 Regular Expression을 한번 귀납적으로 정의해 보겠습니다.

• $\epsilon$은 Regular Expression입니다. (1)
• $\phi$는 Regular Expression입니다. (2)
• $a\in \Sigma$인 $a$는 Regular Expression입니다. (3)
• $R_1, R_2$가 Regular Expression이면 $R_1\cup R_2,\; R_1R_2,\; R_{1}^{*}$는 Regular Expression입니다. (4)

 

그 예시로 아까 봤던 $\left ( 0 \cup 1 \right )1^{*}$가 Regular Expression임을 한번 증명해보겠습니다. 

먼저 (3)에 의해 $0$과 $1$은 Regular Expression이므로, (4)에 의해 $\left ( 0 \cup 1 \right )$는 Regular Expression입니다. 마찬가지로 (4)에 의해 $1^{*}$은 Regular Expression입니다. 따라서, 이 둘을 연결한 $\left ( 0 \cup 1 \right )1^{*}$ 역시 (4)에 의해 Regular Expression입니다.

이렇게 만들어진 Regular Expression $R=\left ( 0 \cup 1 \right )1^{*}$에 대응되는 Language는 $L=\left\{ 0, 01, 011, 0111, 01111,\cdots, 1, 11, 111, 1111, \cdots \right\} $ 였었죠. 이를 $R$이 $L$을 Describe 한다라고 표현합니다.

여기서 서로 다른 두 Regular Expression이 같은 Language를 Descibe 할 수도 있는데요, 예를 들어

$$\left ( 0 \cup \epsilon \right )1^{*}, \; 01^{*}\cup 1^{*}$$

이 두 Regular Expression은 같은 Language를 Describe 함을 쉽게 알 수 있는데요, 이런 상황에서 우리는 이 두 Regular Language는 같다, 수학적으로는 $\left ( 0 \cup \epsilon \right )1^{*}= 01^{*}\cup 1^{*}$ 라고 표현합니다.

 

Regular Expression Identity

Regular Expression은 아래의 성질을 만족합니다.

1. $R_1\phi =\phi R_1=\phi$
2. $R_1\epsilon = \epsilon R_1=R_1$
3. $R_1\cup \phi = \phi \cup R_1 = R_1$
4. $R_1 \cup R_1=R_1$
5. $R_1\cup R_2 = R_2\cup R_1$
6. $R_1\left (R_2 \cup R_3  \right )=R_1R_2 \cup R_1R_3$
7. $\left (R_1\cup R_2 \right )R_3 =R_1R_3\cup R_2R_3$
8. $R_1\left ( R_2R_3 \right )=\left ( R_1R_2 \right )R_3$
9. $\phi^{*}=\epsilon$
10. $\epsilon^{*}=\epsilon$
11. $\left ( \epsilon \cup R_1 \right )^{*}=R_1^{*}$
12. $\left ( \epsilon \cup R_1 \right )\left ( \epsilon \cup \right )^{*}=R_1^{*}$
13. $R_1^{*}\left ( \epsilon \cup R_1 \right )=\left ( \epsilon \cup R_1 \right )R_1^{*}=R_1^{*}$
14. $R_1^{*}R_2 \cup R_2=R_1^{*}R_2$
15. $R_1\left ( R_2R_1 \right )^{*}=\left ( R_1R_2 \right )^{*}R_1$
16. $\left ( R_1\cup R_2 \right )^{*}=\left ( R_1^{*}R_2 \right )^{*}R_1^{*}=\left ( R_2^{*}R_1 \right )^{*}R_2^{*}$

 

성질이 엄청 많은데 하나하나 차근차근 읽어보면 아주 간단한 것들입니다. 이제 이 성질들을 이용하여 두 Regular Expression이 같음, 즉 같은 두 Regular Expression이 같은 Language를 Describe 한다는 것을 보일 수 있습니다.

아까 이 두 Language $\left ( 0 \cup 1 \right )1^{*}, \; 01^{*}\cup 1^{*}$가 같은 Language라고 했었죠? 위 Identity들을 이용해서 이를 증명해 보겠습니다.

먼저, (7)에 의해 $\left ( 0 \cup \epsilon \right )1^{*}=01^{*}\cup \epsilon 1^{*}$ 입니다. 그리고 (2)에 의해 $\epsilon 1^{*} =1^{*}$이므로 $01^{*}\cup \epsilon 1^{*}=01^{*}\cup \1^{*}$임을 알 수 있습니다. 즉, $\left ( 0 \cup 1 \right )1^{*}=01^{*}\cup 1^{*}$ 임이 증명되었습니다.

 

Regular Expression과 Regular Language

이때까지 저희는 Regular Expression에 대해 알아보았고, Regular Expression은 Language를 Describe 한다는 사실에 대해 알아보았습니다. 사실 워딩을 보고 눈치채신 분들도 있겠지만, 어떤 Language를 Describe 하는 Regular Expression이 존재하면 그 Language는 Regular Language입니다. 그 역도 성립하고요.

먼저 Regular Expression이 항상 Regular Language를 Describe 함을 증명해 보겠습니다. 임의의 Regular Expression이 Decribe 하는 어떤 Language가 Regular 함을 증명하려면 어떻게 해야 하죠? 바로 이 Language를 Accept 하는 DFA가 존재함을 보이면 되겠죠.

증명으로는 역시 귀납적인 방법을 사용할 것인데요, 아까 위에서 Regular Expression을 정의할 때 귀납적인 방법을 사용했으므로 이를 따라 똑같이 증명을 진행해나가 보겠습니다.

먼저 (1)에 의해 $\epsilon$은 Regular Expression이므로 이에 대응되는 DFA가 있는지 확인해 보겠습니다.

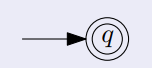
$\epsilon$에 대응되는 DFA

이렇게 Regular Expression $\epsilon$이 Describe 하는 Language $\left\{ \epsilon \right\}$를 Accept 하는 DFA를 간단하게 찾을 수 있습니다. (하나하나 자세히 적기 힘드니 앞으로는 그냥 "$\epsilon$에 대응되는 DFA" 이렇게 간단히 적겠습니다.)

계속 진행해 보면 (2)에 의해 $\phi$는 Regular Expression이고, 이에 대응되는 DFA는 아래와 같습니다.

$\phi$에 대응되는 DFA

다음 Base Case인 (3)에서 $a\in \Sigma$인 $a$는 Regular Expression이고, 이에 대응되는 DFA는 아래와 같습니다.

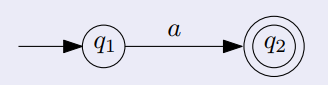
$a$에 대응되는 DFA

 

이제 마지막으로 이 3개의 Base Case가 있으니, Regular Expression $R_1, R_2$이 주어졌을 때 이 3개의 Regular Expression $R_1\cup R_2,\; R_1R_2,\; R_{1}^{*}$이 Describe 하는 Language가 Regular함을 보이겠습니다.

먼저 $R_1, R_2$가 각각 Describe하는 Language를 $L_1, L_2$라고 하겠습니다. 그러면 $L_1, L_2$가 Regular라고 가정했을 때, $L_1 \cup L_2,\; L_1 L_2,\; L_{1}^{*}$가 Regular임을 보이면 그게 바로 Induction Step이겠죠? 그런데 사실 이 내용은 전 글의 마지막 부분에서 증명을 끝낸 내용입니다.

 

따라서, Structural Induction에 의해 Regular Expression이 Describe하는 Language는 항상 Regular임을 증명할 수 있었습니다. 예시로 한번 더 확인해 볼까요?

 

$(ab\cup a)^{*}$라는 Regular Expression이 있다고 생각해 봅시다. 먼저 Base Case인 Regular Expression $a$와 $b$가 Describe 하는 Language를 Accept 하는 $M_1, M_2$는 각각 아래와 같습니다.

그리고 전 글의 마지막 부분에서 사용한 방법을 사용해 $ab$에 대응되는 $M_3$도 아래와 같이 만들 수 있습니다. $\epsilon$이 그려진 화살표를 $M_1$의 Accept State에서 $M_2$의 Start State로 이어주면 되겠죠.

이제 $ab \cup b$에 대응되는 $M_4$를 만들어보겠습니다. 전 글에서 나왔던 방법 그대로, 새로운 Start State를 만들어 $M_1$과 $M_3$를 연결해 주면 됩니다.

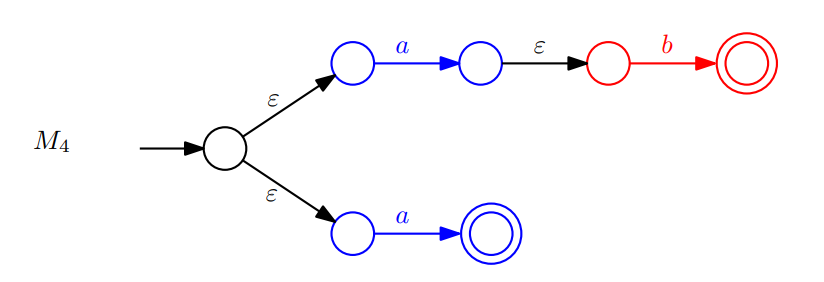
마지막으로 $(ab \cup b)^{*}$에 대응되는 $M_5$는 아래와 같습니다. (방법은 역시 전 글 마지막 부분 그대로입니다.)

이렇게 Regular Expression $(ab \cup b)^{*}$에 대응되는 NFA가 만들어졌으니, 이는 곧 DFA도 존재한다는 것을 의미하고 $(ab \cup b)^{*}$가 Describe 하는 Language는 Regular임을 의미합니다. 이와 똑같은 방식을 이용하면 어떤 Regular Expresison일지라도 대응되는 DFA를 만들 수 있습니다.

 

이제 이때까지 증명했던 명제의 역인, 모든 Regular Language는 Regular Expression으로 변환될 수 있음을 증명해 보겠습니다. 이를 위해서 하나의 보조 정리를 이용할 겁니다.

주어진 Alphabet $\Sigma$에 대해, $\Sigma^{*}$에 대한 Language $B, C, L$이 있다. 이때 $\epsilon \notin B$ 이고 $L=BL\cup C$이면, $L=B^{*}C$이다.

이 Lemma가 가지는 의의는 바로 Language $B, C$는 알고 있고, $L$은 모르는 상태에서 $L=BL\cup C$라는 식이 주어졌을 때, Language $L$을 $B$와 $C$에 대한 식으로 나타낼 수 있다는 것에 있습니다. 일차방정식 푸는 것과 약간 비슷하다고 생각하시면 될 것 같아요.

 

그럼 이제 위 Lemma를 활용해서 Regular Language를 Regular Expression으로 변환하는 과정을 한번 알아보겠습니다. 먼저 어떤 Language가 Regular라는 말은 이 Languege를 Accept 하는 Machine이 존재한다는 뜻이겠죠? 따라서, 위 명제는 어떤 DFA를 Regular Expression으로 변환 가능하다는 것과 같은 의미입니다.

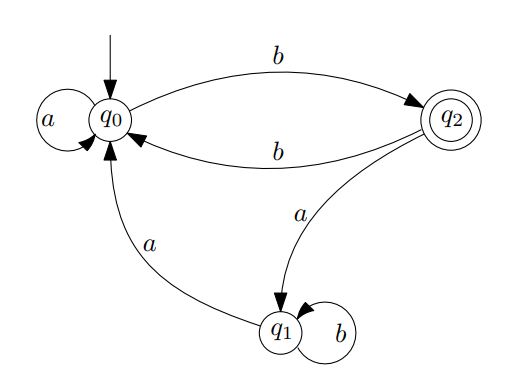
예시로 이런 DFA를 한번 Regular Expression으로 변환해 보겠습니다. 먼저 위 State $r$에서 시작했을 때 위 Machine이 Accept하는 문자열의 집합을 $L_r$이라고 정의하겠습니다. 그러면 위 DFA에는 3개의 State가 있으므로 $L_{q_0}, L_{q_1}, L_{q_2}$를 각각 정의할 수 있습니다.

이때, $L_{q_0}$에 있는 문자열을 2가지로 분류할 수 있습니다. $a$로 시작하는 문자열과 $b$로 시작하는 문자열이죠. 먼저 $L_{q_0}$에 있는 문자열 중 $a$로 시작하는 문자열을 $aT$라고 하겠습니다. ($T$는 문자열) 그러면 $aT$가 $L_{q_0}$의 원소라는 것은, $q_0$에서 $a$를 입력받고 $T$를 입력받으면 Accept State가 된다는 의미입니다. 그런데 $q_0$에서 $a$를 입력받으면 State는 $q_0$잖아요? 따라서, $q_0$에서 $T$를 입력받으면 Accept State가 됩니다. 아까 $q_0$에서 시작했을 때 Accept State가 되는 문자열의 집합을 $L_{q_0}$라고 한다고 했으니까, $T=L_{q_0}$라고 할 수 있습니다.

똑같이 생각해 보겠습니다. $L_{q_0}$에 있는 문자열 중 $b$로 시작하는 문자열을 $bS$라고 하겠습니다. $bS$가 $L_{q_0}$의 원소라는 것은, $q_0$에서 $b$를 입력받고 $S$를 입력받으면 Accept State가 된다는 의미입니다. 그런데 $q_0$에서 $b$를 입력받으면 State는 $q_2$잖아요? 따라서, $q_2$에서 $S$를 입력받으면 Accept State가 됩니다. 아까 $q_2$에서 시작했을 때 Accept State가 되는 문자열의 집합을 $L_{q_2}$라고 한다고 했으니까, $S=L_{q_2}$라고 할 수 있습니다.

즉, $L_{q_0}=a L_{q_0} \cup bL_{q_2} $가 됩니다. 똑같은 방법으로 $q_1, q_2$에 대해서도 생각해 보면, 아래의 식 3개를 얻을 수 있습니다.

• $L_{q_0}=aL_{q_0} \cup bL_{q_2}$
• $L_{q_1}=aL_{q_0} \cup bL_{q_1}$
• $L_{q_2}=aL_{q_1} \cup bL_{q_0} \cup \epsilon$

 

이제 위의 식을 각각 (1), (2), (3)이라고 하고 계산을 해보겠습니다. 먼저 (3)을 (1)에 대입하면,

$$L_{q_0}=aL_{q_0}\cup b\left ( \epsilon \cup aL_{q_1}\cup bL_{q_0} \right )\\ =aL_{q_0} \cup b \cup baL_{q_1}\cup bbL_{q_0} \\ =\left ( a\cup bb \right )L_{q_0} \cup baL_{q_1}\cup b$$

위 식을 (4)라고 하겠습니다. 그러면 $L_{q_2}$가 소거되었습니다. 이제 식 (2)에 Lemma를 적용해서 조금 정리를 해보면 아래의 식을 얻을 수 있습니다.

$$L_{q_1}=b^{*}aL_{q_0}$$

이제 $L_{q_1}$이 $ L_{q_0} $에 대한 식으로 나타내졌으므로, 위 식을 (4)에 대입하면 $L_{q_1}$도 소거시킬 수 있겠죠?

$$L_{q_0}=(a\cup bb)L_{q_0} \cup bab^{*}aL_{q_0}\cup b \\ = (a \cup bb \cup bab^{*}a)L_{q_0}\cup b$$

이제 위 식에 다시 Lemma를 적용하면,

$$L_{q_0}=(a\cup bb \cup bab^{*}a)^{*}b$$

이런 식을 얻을 수 있습니다. $L_{q_0}$의 정의는 "State $q_0$에서 시작했을 때 위 Machine이 Accept 하는 문자열의 집합"이였죠? 그런데 $q_0$가 Start State이므로 $L_{q_0}$는 결국 위 Machine이 Accept하는 문자열의 집합이 되고, $ (a\cup bb \cup bab^{*}a)^{*}b $가 위 DFA에 대응되는 Regular Expression임을 알 수 있습니다.

 

이런 방식으로 모든 DFA를 Regular Expression으로 변환할 수 있습니다. 예시를 통해 설명했지만, 귀납법을 이용하면 모든 DFA를 Regular Expression으로 변환할 수 있음을 보일 수 있습니다. (딱히 설명하진 않겠습니다.)

 

마무리

이번 글에서는 Regular Expression이 무엇인지와 어떤 성질을 가지는지에 대해서 알아보았고, 더 나아가 Regular Expression과 Regular Language 간의 대응 관계에 대해서 알아보고 증명해 보았습니다.

감사합니다.

---

이 글은 컴퓨터공학과 학부생이 개인 공부 목적으로 작성한 글이므로, 부정확하거나 틀린 내용이 있을 수 있으니 참고용으로만 봐주시면 좋겠습니다. 레퍼런스 및 글에 대한 기본적인 정보는 이 글을 참고해 주세요.