[프언] #15. Subtype Polymorphism
이번 글에서는 Type System을 Record에도 적용되도록 확장해 보겠습니다. 편의성을 위해, 프로시져에 대해서는 Type Annotation을 사용하도록 하겠습니다.

이 2개의 Expression에 대한 Typing Rule을 적용하는 것 자체는 정말 간단합니다.


Limitation
하지만 역시 이도 한계점이 존재합니다. 먼저 이렇게 만들어진 Type System은 Sound입니다.
let f = proc x: {z: int} x.z in (f {z = 10, y = 9})위 코드에서 프로시져 f는 Record를 하나 받아 그 Record의 z값을 리턴합니다. 따라서 위 코드는 10으로 계산되지만, Type System은 프로시져 f의 입력값을 {z: int} 형태의 Record로 특정하기 때문에 Type Error가 발생합니다.
이런 종류의 문제점을 해결하기 위해 여기에서도 Polymorphism을 이용합니다.
Subtype
Subtype은 두 Type간의 상관관계를 나타내기 위해 사용됩니다.
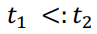
위와 같이 적으면, 이는 $t_2$가 사용되는 곳에 $t_1$이 대신 사용되어도 아무 문제가 없다는 것을 의미합니다. 이때 $t_1$을 $t_2$의 Subtype, $t_2$는 $t_1$의 Supertype이라고 합니다. 위의 예시와 같은 상황에서 {z: int, y:int} 대신에 {z: int}를 사용해도 된다는 것을 표현하기 위해, 아래와 같이 적을 수 있습니다.

그리고 아래와 같은 Typing Rule을 추가함으로서, 위와 같은 문제를 해결할 수 있습니다.

Subtype의 성질
이제부터는 Subtype의 성질에 대해 알아보겠습니다. 먼저, 어떤 Type은 그 자신의 Subtype이며 Supertype입니다. (Reflexivity) 즉, 아래가 성립합니다.

그리고, 만약 $t_1 <: t_2,\quad t_2 <:t_3$이면 $t_1 <: t_3$ 입니다. (Transitivity) 이를 Inference Rule로 나타내면 아래와 같습니다.

그리고 일반적으로, 어떤 Record r이 있을 때 r에 field를 추가해서 만든 r'은 r의 Subtype입니다. (Width Rule) 그 예시로는 아래와 같은 게 있겠죠.

일반적으로 {x: int}가 들어갈 자리에 {x: int, y: int}를 넣어도 문제가 없음을 나타냅니다.
let f = proc x : {y: int z:int} x.z in (f {z = 10, y = 9})위 코드를 보겠습니다. 위 코드는 실행에 아무런 문제가 없지만, 저희가 지금까지 살펴본 Subtype의 성질만을 이용하면 Type Checking을 통과하지 못할 것으로 보입니다. 이를 위해 아래와 같은 Permutation Rule을 도입합니다.

이는 두 Record의 Field 구성이 동일하다면 한 Record Type은 다른 하나의 Subtype임을 의미합니다.
let f = proc x: {x: {x: int}} x.x.x in (f {x = {x = 10, y = 10}})이제 위 코드를 보겠습니다. 위 코드는 10으로 실행되지만, Type Checking에는 실패합니다. 프로시져의 type은 {x: {x: int}} → int인데 반해, 입력값으로 {x: {x: int, y: int}}가 주어졌기 때문입니다.

즉, 위의 Type Rule이 성립하지만 저희는 아직 이에 대한 이유를 제시할 수 없었습니다. 위가 성립하는 근본적인 이유는 {x: int, y: int}가 {x: int}의 Subtype이기 때문입니다. 따라서, 아래와 같은 Depth Rule을 도입합니다.

프로시져에 대한 Subtype
let f = proc x: {y: int, z: {a: int}} x.z in ...
let g = proc x: {y: int, z: {a: int}} {a := 1, b := 2} in ...위 두 프로시져를 보겠습니다. f의 Type은 {y: int, z: {a: int}} → {a: int}}이고, g는 {y: int, z: {a: int}} → {a: int, b: int}}입니다. 그러면 g를 사용해야 할 자리에 f를 사용해도 Type Checking에 문제가 없을까요? 그렇습니다. 이에 착안해 아래와 같은 Inference Rule이 항상 성립한다고 할 수 있습니다.

만약 반대로, 프로시져의 Argument가 서로 Subtype, Supertype 관계이면 이 관계가 성립할까요? 그렇습니다. 따라서, 아래도 성립합니다.

이 둘을 합쳐서, 아래와 같이 쓸 수 있습니다.

Top Type과 Bottom Type
if (iszero 0) then 1 else iszero 2위와 같은 코드는 Type Checking을 통과하지 못하지만 실제 실행에는 아무 문제가 없습니다.
if (iszero 0) then {a := 10} else {a := 20, b := 20}하지만 위와 같은 코드는 비슷한 문제가 있음에도 Type Checking을 통과할 수 있습니다. 공통된 SuperType이 있기 때문이죠. 이에 착안해서, 모든 Type에 대한 Supertype인 Top Type을 도입할 수 있습니다.

이를 사용하면 첫번째 프로그램도 Type Checker를 통과합니다.
비슷하게, 모든 Type에 대한 Subtype인 Bottom Type도 도입할 수 있습니다.

Bottom Type에 대해 자세히 다루지는 않겠지만, 예외 처리를 할 때 등 사용처가 있긴 합니다.
감사합니다.
이 글은 컴퓨터공학과 학부생이 개인 공부 목적으로 작성한 글이므로, 부정확하거나 틀린 내용이 있을 수 있으니 참고용으로만 봐주시면 좋겠습니다. 레퍼런스 및 글에 대한 기본적인 정보는 이 글을 참고해 주세요.