[계산이론] #16. Chomsky Normal Form
Chomsky Normal Form이란?
어떤 Context-Free Grammar의 $R$이 아래 조건을 만족하는 Rule로만 구성되어 있을 경우, Chomsky Normal Form이라고 합니다.
- $A\to BC$, where $A, B, C\in V$, $B \neq S$, $C \neq S$
- $A \to a$, where $A \in V$ and $a \in \Sigma$
- $S \to \epsilon$
Chomsky Normal Form으로의 변형
어떤 임의의 Context-Free Language가 있을 때, 이 Language에 대한 Chomsky Normal Form인 Context-Free Grammar가 항상 존재합니다. 다시 말해, 임의의 Context-Free Grammar는 Chomsky Normal Form으로 변형이 가능합니다.
임의의 Context-Free Grammar를 Chomsky Normal Form으로 변형하는 과정은 크게 5단계로 나뉘는데요, 하나하나 살펴보도록 하겠습니다.
이해를 돕기 위한 예시로, $V=\left\{A, B \right\}, \Sigma = \left\{ 0,1 \right\}$이며 $R$이 아래와 같은 Context-Free Grammar를 이용하겠습니다.

1. 우변에 있는 Start Variable을 전부 없앱니다.
먼저 Chomsky Normal Form의 첫 번째 규칙에 의해 우변에 오는 Variable은 Start Variable이 아니여야 합니다. 이 단계는 간단합니다. 새로운 Start Variable $S_1$을 만들고, Rule에 $S_1 \to S$를 추가해 주면 됩니다. 그러면 우변에 $S$가 존재하더라도 이제 $S$는 더 이상 Start Variable이 아니므로 조건을 만족합니다.
저희의 예시에도 새로운 Variable인 $S$와 $S\to A$를 추가해줍니다.

2. $A \to \epsilon$ 형태의 Rule을 없앱니다. ($\epsilon$-Rule)
$A \to \epsilon$을 없애고 싶다고 가정합시다. 이 Rule은 그냥 제거할 수 없기 때문에 아래와 같은 처리를 해주어야 합니다.
- $B \to A$가 있을 경우 $B\to \epsilon$을 추가합니다. 그러면 $B\Rightarrow A \Rightarrow \epsilon$이였던 단계가 $B \Rightarrow \epsilon$이 되므로 Grammar가 만들어내는 Language에 영향을 주지 않습니다. 단, $B \to \epsilon$을 이전에 이미 제거했었다면 추가하지 않아도 됩니다.
- $B \to uAv$가 있을 경우 $B \to uv$를 추가합니다.
- $B \to uAvAw$가 있을 경우 $B \to uvw$, $B \to uAvw$, $B \to uvAw$를 추가합니다.
- 우변에 $A$가 3번 이상 존재하는 Rule에도 비슷한 처리를 할 수 있습니다.
이렇게 $A$에 대한 모든 처리가 끝났다면, 다음 $\epsilon$-Rule을 없애고, 처리를 하고, 이를 반복해 주면 언젠가 $S \to \epsilon $만 남게 되겠죠.
저희의 예시에서는 먼저 $A\to \epsilon$을 제거해 줄 겁니다. 먼저 $S\to A$가 있기 때문에 $S\to \epsilon$을 추가해 줍니다. 그리고 $A\to BAB$가 있기 때문에 $A\to BB$를 추가해줍니다.

그리도 다음 단계로 $B\to \epsilon$도 제거해 줍니다.
먼저 $A \to B$가 있기 때문에 $A\to \epsilon$을 추가해야 하지만, 이미 이전 단계에서 $A\to \epsilon$을 제거했기 때문에 추가할 필요가 없습니다. 그다음으로 $A\to BAB$가 있기 때문에 $A\to A$, $A\to AB$, $A\to BA$를 추가해 줍니다.

3. $A\to B$ 형태의 Rule을 없앱니다. (Unit-Rule)
$A \to B$를 없애고 싶다고 가정합시다. 이를 없애기 위해 $R$에 존재하는 $B\to u$ 형태의 모든 Rule에 대해 $A\to u$를 추가해 주면 됩니다. 단, 이미 제거했었다면 추가하지 않아도 됩니다.
이렇게 $A \to B$에 대한 모든 처리가 끝났다면, 다음 Unit-Rule을 없애고, 처리를 하고, 이를 반복해 줍니다.
저희의 예시에서는 먼저 $A\to A$를 없애줍니다. 이 Rule은 아무 처리 없이 그냥 없애도 결과에 아무 영향이 없습니다.

다음으로 $S\to A$를 없애주어야 하는데, 이를 없애기 위해선 $S\to BAB\;|\;B\;|\;BB\;|\;AB\;|\;BA$를 추가해줘야 합니다.

이제 다음 Unit-Rule인 $S\to B$를 없애줍니다. $S\to 00$만 추가해 주면 되겠죠.

이제 마지막 Unit-Rule인 $A\to B$를 없애주기 위해 $A\to 00$을 추가합니다.

4. 우변에 3개 이상의 Symbol이 존재하는 Rule을 없앱니다.
$A \to u_1u_2 \cdots u_k$를 없애고 싶다고 가정합시다. 이를 없애기 위해 아래와 같은 Rule을 추가해주어야 합니다.

저희의 예시에서는 $S\to BAB$, $A\to BAB$를 없애주어야 합니다.
$S\to BAB$를 없애기 위해 $S\to BA_1$과 $A_1\to AB$를 추가해 주고, $A\to BAB$를 없애기 위해 $A\to BA_2$, $A_2\to AB$를 추가해 주면 아래와 같습니다.

5. $A \to u_1u_2$ 형태의 Rule을 없앱니다. ($u_1$과 $u_2$ 둘 다 Variable이 아닌 경우)
$A \to u_1u_2$를 없애고 싶다고 가정합시다. 이를 없애기 위해 아래와 같은 처리를 해주어야 합니다.
- $u_1\in V$이고 $u_2\in V$이면 이 Rule은 Chomsky Normal Form의 문법에 맞기 때문에 없앨 필요가 없습니다.
- $u_1\in \Sigma$이고 $u_2 \in V$이면 새로운 Variable $U_1$을 만들어 $A\to U_1u_2$와 $U_1\to u_1$을 추가해 줍니다. 그러면 Chomsky Normal Form의 문법에 맞는 Rule만 남습니다.
- $u_1\in V$이고 $u_2 \in \Sigma$이면 새로운 Variable $U_2$를 만들어 $A\to u_1U_2$와 $U_2\to u_2$를 추가해줍니다. 그러면 Chomsky Normal Form의 문법에 맞는 Rule만 남습니다.
- $u_1, u_2 \in \Sigma$이고 $u_1 \neq u_2$이면, 새로운 Variable $U_1, U_2$를 만들어 $A\to U_1U_2$와 $U_1\to u_1$, $U_2\to u_2$를 추가해줍니다. 그러면 Chomsky Normal Form의 문법에 맞는 Rule만 남습니다.
- $u_1, u_2 \in \Sigma$이고 $u_1 = u_2$이면, 새로운 Variable $U_1$을 만들어 $A\to U_1U_1$와 $U_1\to u_1$을 추가해줍니다. 그러면 Chomsky Normal Form의 문법에 맞는 Rule만 남습니다.
저희의 예시에서는 아래와 같은 처리가 필요합니다.

그 결과는 아래와 같습니다.

이 Grammar는 Chomsky Normal Form을 만족합니다.
Pushdown Automata

새로운 개념인 Pushdown Automata를 소개합니다. 이는 2-tape TM으로 첫 번째 Tape은 항상 오른쪽으로 움직이며 Read-Only입니다. 그리고 두 번째 Tape은 Stack과 같이 작동합니다. Stack의 상단에 Symbol을 추가하거나 (Push) 상단에 있는 Symbol을 제거하거나 (Pop) 2가지 연산이 가능합니다.
Tape, Cell, Tape Alphabet ($\Sigma$), Blank Symbol, Tape Head, State Control ($Q$), Start State ($q$) 등의 용어는 Turing Machine을 다룰 때와 동일합니다. 새로 추가된 Stack의 경우, Stack Alphabet ($\Gamma $)를 사용합니다. $\Gamma$에는 새로운 Special Symbol인 #이 존재합니다.
초기 조건은 다음과 같습니다. Pushdown Automata의 Input은 Tape에 저장되어 있습니다. Tape Head는 가장 왼쪽에 위치해 있으며, Stack에는 단 한 개의 Symbol #만 존재합니다. 그리고 State는 $q$입니다.
하나의 Computation Step에서 먼저 Pushdown Automata는 Tape Head에서 읽은 Symbol, Stack Head에서 읽은 Symbol, 그리고 현재 State를 바탕으로 다음 3가지 일을 수행합니다.
- State를 업데이트합니다.
- Tape Head가 한 칸 움직이거나, 그 자리에 가만히 있습니다.
- Stack에 새로운 Symbol을 추가하거나 Symbol이 제거됩니다.
Properly Nested Parentheses
Pushdown Automaton의 첫 예시로 Properly Nested Parentheses에 대해 알아보겠습니다. 다들 아실만한 간단한 문제입니다. 모든 Properly Nested Parentheses를 포함하는 언어를 $L$이라고 하면 (()())()는 $L$의 원소이지만 (()))(()는 $L$의 원소가 아닙니다.

이것이 초기 상태이겠죠. (a는 여는 괄호 '('를, b는 닫는 괄호 ')'를 나타내는 기호입니다.) 먼저 이 상태에서 a가 읽어지기 때문에, Stack에 임의의 원소 S를 하나 추가합니다.
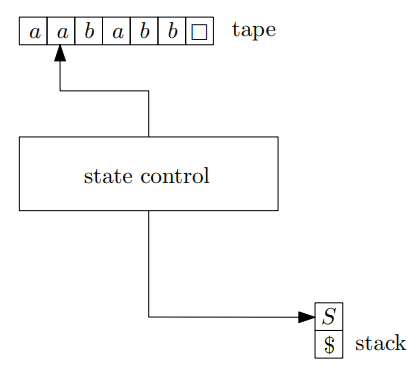
이 상태가 됩니다. 또 한 번 a가 읽히므로 S를 하나 추가합니다.

그러면 이 상태가 됩니다. 여기서 Stack에 S가 2개 들어갔다는 것은, 현재 상태에서 열려있는 괄호가 총 2개 남아있다는 것을 의미합니다. 이번에는 b가 읽히는데, 이는 괄호를 하나 닫는다는 것을 의미하므로 Stack에서 S를 하나 제거합니다.

이제 다시 a가 읽히므로 S를 하나 추가합니다.

이제 b가 2번 읽히기 때문에 S가 2번 제거되겠죠.

Tape의 끝에 도달했는데, Stack에 남은 S가 없습니다. 즉, 열려있는 괄호가 없다는 것을 의미하므로 Input이 Properly Nested임을 알 수 있습니다. 따라서 이 Pushdown Automata는 주어진 Input을 Accept 합니다.
이를 수학적인 표현으로 바꾸면 아래와 같습니다.

Transition Function $\delta$는 아래와 같습니다.

a를 입력받았을 때 Stack에 S를 추가하라는 의미입니다.

b를 입력받았을 때 Stack에서 S를 제거하라는 의미입니다.

b를 입력받았을 때 Stack에서 읽히는 Symbol이 S가 아니라 #라는 것은 현재 입력받은 a의 개수보다 b의 개수가 많다는 것을 의미합니다. 즉, 괄호가 똑바로 묶이지 않았다는 것이므로 Input이 Reject 됩니다.


만약 입력을 전부 처리했는데 Stack이 비어있다면 Input을 Accept 합니다. Stack이 비어있지 않다면 a의 개수가 b의 개수보다 많다는 것을 의미하므로 Input을 Reject 합니다.
왜 위의 기호들이 Accept와 Reject를 의미하는지 궁금하실 겁니다. Pushdown Automata는 Stack이 빈 상태가 되었을 때 Terminate 됩니다. 그리고 위와 같이 Terminate 됨과 동시에 Tape Head가 마지막 Symbol에서 Blank Symbol으로 넘어갈 경우, 이 Pushdown Automata는 Input을 Accept 합니다.
무한 루프에 빠져서 Input을 전부 읽지 못하거나, Stack이 비어 Terminate 됨과 동시에 Tape Head가 마지막 Symbol에서 Blank Symbol로 넘어가지 않을 경우 Reject 됩니다.
Non-Deterministic Pushdown Automata
지금까지 다루었던 Pushdown Automata는 Deterministic입니다. Non-Deterministic Pushdown Automata에서는 어떠한 상태에서 가능한 Computation Step이 하나가 아닐 수 있습니다. Automata가 그중 하나를 선택해서 실행할 수 있죠. NFA/DFA의 예시에서 보았듯이, 가능한 모든 경우의 수 중에 Input을 Accept 하는 경우의 수가 하나라도 존재하는 경우 Input을 Accept 한다고 합니다. 만약 모든 경우의 수가 전부 Input을 Reject 한다면 Automata는 Input을 Reject 합니다.
Pushdown Automata의 다른 예시
길이가 홀수이며 가장 가운데에 있는 문자가 b인 언어를 생각해 보겠습니다. 예를 들어 aabba, abababa는 이 언어의 원소이지만, aaabb, aabb 등은 이 언어의 원소가 아닙니다.
이 문제는 Non-Deterministic Pushdown Automata로 해결 가능합니다. 기본적인 아이디어는 2개의 State q, q'이 있고 중앙에 도달하면 State가 q'으로 바뀌는 겁니다.

Pushdown Automata와 Context-Free Grammar
$V=\left\{S,A,B \right\},\Sigma =\left\{a,b \right\}$이고 Rule이 아래와 같은 Chomsky Normal Form의 Grammar를 봅시다.
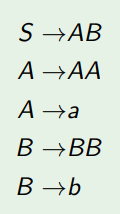
이 Rule으로부터 aaaabb를 얻어낼 수 있습니다.


이 그래프에 대해 In-Order Travel을 수행하면 아래와 같은 모습입니다.

이에 착안해서, 초기에 aaaabb를 얻은 방법과는 다른 방법을 이용해서 aaaabb를 얻을 수 있습니다.

이런 방식을 Left to Right라고 합니다.
조금 일반적으로, 저희가 Chomsky Normal Form을 사용하여 어떤 문자열을 얻어낼 때 Left to Right 한 방법을 사용할 수 있습니다. 매번 Rule을 적용시킬 때, 가장 왼쪽에 있는 Variable에만 Rule을 적용하는 것입니다.
이 방법을 이용하면, 모든 Chomsky Normal Form의 Context-Free Grammar는 Non-Deterministic Pushdown Automata로 변환 가능합니다. 지금부터 그 과정을 차근차근 살펴보도록 하겠습니다.

이런 Context-Free Grammar가 있다고 가정합시다. 아시다시피, 이 Grammar는 Chomsky Normal Form입니다. 이때 L(G)를 Accept 하는 Automaton $M$을 한번 만들어보겠습니다.

위와 같은 변환 식에서, Left to Right 한 방법을 이용하면 각 단계를 아래와 같이 표기할 수 있습니다.

그러니까 처음 시작할 때의 조건을 $i=1$, $k=1$로 나타낼 수 있으며, 최종 단계는 $i=n+1$, $k=0$으로 나타낼 수 있겠습니다. 이때, 저희가 만들 Pushdown Automaton은 아래와 같은 형태입니다.

이 상태에서 $A_k$에 어떤 Rule이 적용될 텐데, 그 Rule은 아래 3가지 중 하나일 것입니다.
- $A\to BC$ : Instruction $qaA\to qNCB$가 실행됩니다.
- $A\to a$ : Instruction $qaA \to qR\epsilon$이 실행됩니다.
- $\$ \to \epsilon$ : Instruction $q \square \$ \to qN\epsilon$이 실행됩니다.
이와 같이 작동하는 Pushdown Automaton은 L(G)의 모든 원소를 Accept 하므로 Chomsky Normal Form의 Context-Free Grammar는 Non-Deterministic Pushdown Automata로 변환 가능하다는 것이 증명되었습니다.
여기서 증명을 다루지는 않겠지만, 반대로 Non-Deterministic Pushdown Automata를 Chomsky Normal Form의 Context-Free Grammar로 변환할 수도 있습니다. 여기에서 모든 Context-Free Language는 Chomsky Normal Form의 Grammar를 갖기 때문에, 아래가 성립합니다.
Context-Free Language $\Leftrightarrow $ $L$ Accepted by Non-Deterministic Pushdown Automaton
이렇게 순서가 조금 바뀌긴 했지만, 계산이론 교재에 있는 모든 내용을 다루었습니다.
감사합니다.
이 글은 컴퓨터공학과 학부생이 개인 공부 목적으로 작성한 글이므로, 부정확하거나 틀린 내용이 있을 수 있으니 참고용으로만 봐주시면 좋겠습니다. 레퍼런스 및 글에 대한 기본적인 정보는 이 글을 참고해 주세요.