[계산이론] #15. Context-Free Language
이전까지의 글에서 저희는 Complexity Theory에 대해 알아보았습니다. 이번 글에서는 다시 Regular Language로 살짝 돌아와 보도록 하겠습니다.
Context-Free Language
이번 글에서 저희는 Context-Free Language에 대해 알아볼 것입니다. Context-Free Language는 $\textbf{P}$의 부분집합이며, Regular Language의 상위 집합입니다. 즉, 아래가 성립합니다.
$$Regular\; Language \subseteq Context-Free\; Language \subseteq \textbf{P}$$
지난번에 다루었던 가장 대표적인 Nonregular Languge로는 $\left\{0^n1^n:n\geq 0 \right\}$ 같은 것들이 있었는데요, 나중에 다루겠지만 이 언어는 Regular Language는 아니지만 Context-Free Language입니다.
Context-Free Grammar란?
Context-Free Language를 정의하기 전에, 핵심 개념이 되는 Context-Free Grammar에 대해 먼저 알아보도록 하겠습니다. Context-Free Grammar는 기본적으로 아래와 같은 Substitution Rule로 구성됩니다.

여기서 $S,A,B$ 처럼 대문자들은 Variable, $a, b$와 같은 소문자들은 Terminal이라고 부릅니다. $S$는 Start Variable이라고 부릅니다. 위와 같은 Substitution Rule을 이용해 Start Variable인 $S$로부터 문자열을 얻어낼 수 있습니다.

왼쪽은 문자열 aaaabb를 Substitution Rule로 얻어내는 과정이고, 오른쪽은 도표로 그 과정을 나타낸 것입니다. 이렇게 도표로 나타낸 것을 Parse Tree라고 부릅니다. 이것이 Context-Free Grammar의 기본적인 개념입니다. 명칭에서 예상하셨겠지만, Start Variable에서 Context-Free Grammar로 얻어지는 문자열의 집합을 Context-Free Language라고 부르는 겁니다. 제가 예시로 들었던 Grammar는 아래 Language를 나타냅니다.

아시다시피, 위 Language는 Regular입니다. 당연히 Context-Free이기도 하고요.
이제 Context-Free Gramar의 수학적 표현에 대해 알아보겠습니다. Context-Free Grammar는 아래와 같은 4-Tuple로 표현됩니다.
$$G=\left ( V,\Sigma,R,S \right )$$
- $V$는 Variable들의 집합입니다.
- $\Sigma$는 Terminal들의 집합입니다.
- $V\cap \Sigma=\phi $
- $S$는 $V$의 원소로, Start Variable입니다.
- $R$은 Rule의 집합입니다. 각 Rule은 $A\to w,\; where; A\in V,\; w\in \left ( V \cup \Sigma \right )^*$ 입니다.
Context-Free Grammar에 있는 Rule을 한번 사용해 $u$를 $v$로 바꿀 수 있다면, 이를 $v$는 $u$로부터 One Step에 유도 가능하다 (Derived in one step)고 하며, $u\Rightarrow v$로 표현합니다. 예를 들어, 위의 예시에서는 $aaAbb \Rightarrow aaaAbb$ 입니다.
한 번이 아니라 1번 이상 사용해서 $u$를 $v$로 바꿀 수 있다면, 이를 $v$는 $u$로부터 유도 가능하다고 하며, $u \overset{*}{\Rightarrow}v$로 표현합니다. 예를 들어, 위의 예시에서는 $aaAbB \overset{*}{\Rightarrow}aaaabbbB$ 입니다.
이제 이 표현을 이용해 아래와 같이 Context-Free Language $L\left( G \right)$를 정의할 수 있습니다.
$$L\left ( G \right )=\left\{w\in \Sigma^*:S \overset{*}{\Rightarrow}w \right\}$$
Example of Context-Free Language
$$L_1=\left\{0^n1^n:n\geq 0 \right\}$$
아까 언급만 했던 Language인데요, 이 Language가 Context-Free임을 보이려면 이 Language에 대응되는 Context-Free Grammar를 만들면 됩니다. 이 Grammar는 아래와 같이 작동합니다.

간단한 내용이기 때문에 따로 설명은 하지 않겠습니다.
조금 더 복잡하게, $L_2=\left\{1^n0^n:n\geq 0 \right\}$ 으로 정의하고 $L_1$과 $L_2$의 합집합을 $L$이라고 해보겠습니다. 이 언어는 Context-Free일까요? 그렇습니다.

위 Context-Free Grammar는 (사실 이렇게 Rule만 나열하는 것이 아니라 $V, \Sigma$에 대한 정의도 있어야 하지만 편의상 생략하겠습니다.) $L$에 대응되므로 $L$ 역시 Context-Free Language라 할 수 있습니다.
그러면 $L_1$의 Complement, 즉 $0^n1^n$ 형태가 아닌 모든 문자열의 집합은 Context-Free일까요? 이 역시 그렇습니다. $L_1$의 Complement에 속하는 문자열은 아래와 같이 3가지 종류가 있습니다.
- $0^m1^n$ 형태의 문자열 (단, $m < n$)
- $0^m1^n$ 형태의 문자열 (단, $n < m$)
- 10을 포함하는 모든 문자열
하나하나 살펴보겠습니다. 먼저 1번에 해당하는 문자열의 경우 아래와 같은 Rule로 나타낼 수 있습니다.

2번에 해당하는 문자열도 같은 방법으로 나타낼 수 있습니다.

3번에 해당하는 문자열을 나타내기 위해, 아래와 같이 모든 문자열을 유도할 수 있는 Rule $X$를 만들 겁니다.

이 Rule에 따르면 $X$는 모든 문자열을 유도할 수 있으므로, 3번에 해당하는 문자열은 $X10X$의 형태를 띱니다. 따라서, 3번에 해당하는 문자열은 아래와 같이 나타낼 수 있습니다.

이제 마지막으로, 이 3개의 경우를 전부 합쳐주면 $L_1$의 Complement에 대한 Context-Free Grammar가 완성됩니다.

다음으로는 아래와 같은 Language를 보겠습니다.

이 Language 역시 Regular 하지 않지만 Context-Free입니다. 위 언어를 나타내는 Grammar는 아래와 같이 동작합니다.
먼저 $a$를 추가할 때마다 $c$를 하나씩 추가합니다. 그러면 $a^nc^n$을 얻을 수 있습니다. 이 상태에서 이제 $b$를 추가하기 시작하는데, 이 때도 똑같이 $c$를 하나씩 추가합니다. 이를 수학적 표현식으로 나타내면 아래와 같습니다.

여기서 $S\Rightarrow A\Rightarrow B\Rightarrow \epsilon$이므로, 아래와 같이 단순화할 수 있습니다.

사실, Start Variable $S$도 필요가 없습니다. 그냥 $A$를 Start Variable로 잡아버리면 그만이기 때문이죠.

Regular Vs. Context-Free
계속 언급해 왔듯, 모든 Regular Language는 Contex-Free 합니다. 이제부터 그 증명을 해보겠습니다. 어떤 언어 $L$이 Reulgar라는 것은, 이 Language에 대한 DFA가 존재한다는 뜻이겠죠. 어떤 DFA가 주어지더라도 그 DFA를 Context-Free Grammar로 바꿀 수 있다면 모든 Regular Language가 Contex-Free 하다는 것을 증명할 수 있겠죠.
예시로, 101을 포함하는 모든 문자열을 Accept 하는 DFA $M$은 아래와 같습니다.
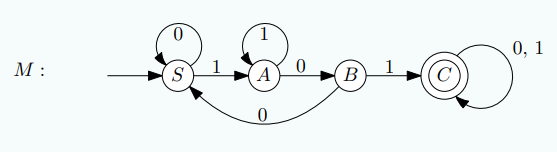
이 $M$은 아래와 같은 Context-Free Grammar로 변환됩니다.

변환 과정에서 크게 어려운 부분은 없고 직관적으로 변환이 가능하다 보니 자세한 설명은 생략하겠습니다.
감사합니다.
이 글은 컴퓨터공학과 학부생이 개인 공부 목적으로 작성한 글이므로, 부정확하거나 틀린 내용이 있을 수 있으니 참고용으로만 봐주시면 좋겠습니다. 레퍼런스 및 글에 대한 기본적인 정보는 이 글을 참고해 주세요.
