[계산이론] #10. P-NP (1)

지금까지 저희는 무슨 문제가 계산 가능한지에 대해 중점적으로 알아보았습니다. 지금부터는, 이런 문제들이 얼마나 빠른 시간 내에 계산 가능한지에 대해 알아보도록 하겠습니다. 이런 문제를 우리는 Complexity Theory라고 합니다.

 

Running Time

Turing Machine $M$에 Input $w$를 집어넣었을 때, 실행되는 Computation Step의 개수를 Running Time이라고 하며 $t_M\left ( w \right )$라고 표시합니다.

여기서 $\mathbb{N}_0$에서 $\mathbb{N}_0$로의 함수 $T$를 아래와 같이 정의합니다.

$$t_M\left ( w \right )\leq T\left ( \left|w \right| \right )$$

이 함수는 특정 길이를 가진 문자열을 $M$이 받았을 때 최소 이 시간 안에는 이 문자열을 처리할 수 있다는 것을 나타내줍니다.

만약 $\Sigma^{*}$에서 $\Sigma^{*}$로의 함수 $F$가 있다고 합시다. 이 때 $w$를 받아 $F\left ( w \right )$를 출력하는 Turing Machine $M$이 존재한다면 이 함수 $F$를 Computable하다고 합니다.

그리고 Turing Machine $M$이 모든 문자열 $w$에 대해 $t_M\left ( w \right )\leq T\left ( \left|w \right| \right )$ 를 만족한다면, 우리는 이 Turing Machine이 함수 $F$를 $T$ 안에 계산한다고 표현합니다. 영어로는 $M$ computes the function $F$ in time $T$ 라고 합니다.

 

이 글에서 저는 어떤 문자열이 Palindrome인지 아닌지를 구분하는 Turing Machine을 소개했었습니다. 이 Turing Machine은 문자열을 왕복하면서 제일 앞에 있는 문자를 지우고, 제일 뒤에 있는 문자를 지우는 것을 반복하면서 작동합니다. 따라서, 길이가 $n$인 문자열이 Palindrome인지 아닌지를 판단하기 위해서는 $n+\left ( n-1 \right )+ \cdots +2+1$번의 연산이 필요합니다.

이를 저희는 간단하게 위 알고리즘의 Running Time은 $O\left ( n+\left ( n-1 \right )+ \cdots +2+1 \right ) $이라고 표현합니다. 더 간단하게 $O\left ( n^2 \right )$라고도 줄일 수 있습니다. ($n$의 값이 매우 커지면 커질수록 $n$의 증가량에 비해 $n^2$의 증가량이 비약적으로 크기 때문에, $n^2$이 항에 포함되어 있으면 $n$이 포함된 항은 무시하는 겁니다.)

위 Turing Machine과 같은 기능을 하지만, 2개의 Tape으로 이루어진 Turing Machine도 다루었었는데요. 이 Turing Machine의 Running Time은 $O\left ( n \right )$으로 이전의 TM보다 더 빠릅니다. 1개의 Tape만 이용해서 $O\left ( n^2 \right )$보다 빠른 Running Time을 가진 알고리즘은 존재하지 않습니다.

당연한 거겠죠? 공간을 덜 쓰는 대신에 시간은 더 쓰고, 공간을 더 쓰는 대신에 시간을 덜 쓰는 것이죠. k-tape TM으로 $T$시간에 해결 가능한 함수는 one-tape TM으로는 $T^2$시간에 해결 가능합니다. one-tape TM으로 $T$시간에 해결 가능한 함수는 C++ 프로그램을 사용하면 $T^2$시간에 해결 가능하고요.

 

Complexity Class P

어떤 알고리즘 $M$이 Running Time $O\left ( n^k \right )$에 해결 가능하다면, 이를 Polynomial Time에 있다고 합니다. 방금 C++ 프로그램, k-tape TM, one-tape TM 사이에서 Running Time의 상관관계에 따라, 이 셋 중에 하나를 이용해 Polynomial Time에 해결 가능한 언어는 나머지 3개로도 Polynomial Time에 해결 가능하다는 것을 쉽게 알 수 있습니다.

Polynomial Time 안에 Decidable한 언어의 집합을 보통 $\textbf{P}$라고 부르며, Polynomial Time안에 Computable한 함수의 집합을 $\textbf{FP}$라 줄여서 부릅니다. 예를 들어, Palindrome의 집합 $Pal$은 one-tape TM을 통해 $O\left ( n^2 \right )$ 시간에 해결 가능하므로, $Pal \in \textbf{P} $라고 할 수 있습니다.

 

P : 2-Coloring Problem

$\textbf{P}$에 대해 조금 더 복잡한 예시를 한번 보겠습니다.

이렇게 그래프의 꼭짓점들을 색칠할건데요, 2가지 규칙을 지켜야 합니다. 첫번째 규칙은 서로 이웃한 꼭짓점에는 다른 색이 칠해져야 한다는 것이고, 두번째 규칙은 단 2개의 색만 사용해 모든 꼭짓점을 색칠해야 한다는 것입니다. 이런 규칙으로 색칠할 수 있는 그래프를 2-colorable이라고 하겠습니다.

그 예시로 위 그림에서 $G_1$은 2-colorable이지만, $G_2$는 그렇지 않습니다. 이렇게 2-colorable한 그래프의 이진 표현, $\left<G \right>$의 집합을 $2Color$라고 하겠습니다. 이제 이 집합이 $\textbf{P}$의 부분집합임을 확인해보도록 하겠습니다.

이런 그래프를 입력받았다고 생각해봅시다. 그러면 일단 임의로 1번 꼭짓점을 빨간색으로 칠합니다.

이제 이 상황에서 1번 꼭짓점과 연결된 꼭짓점들은 빨간색 말고 다른 색으로 칠해야 하기 때문에 선택지가 하나밖에 남지 않습니다. 따라서 2번, 3번, 4번 꼭짓점을 파란색으로 칠합니다.

이제 1번 꼭짓점과 1번 꼭짓점에 연결된 꼭짓점은 모두 규칙에 맞게 색칠했으니, 1번 꼭짓점은 완성된겁니다. 이렇게 완성된 꼭짓점은 굵은 원으로 표시하겠습니다.

이제 그 다음으로 2번 꼭짓점으로 이동해서, 이 과정을 반복합니다. 2번 꼭짓점은 파란색이므로 연결된 6번 꼭짓점은 빨간색으로 칠해야 합니다.

2번 꼭짓점도 완성되었으니 굵은 원으로 표시했습니다. 이제 3번 꼭짓점입니다.

4번 꼭짓점은 이미 완성되어 있으니 바로 굵은 원으로 표시해주겠습니다.

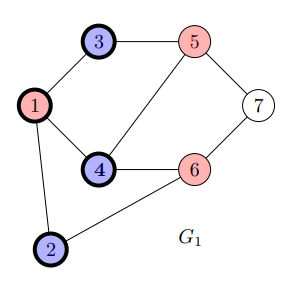
5번 꼭짓점도 규칙에 따라 완성시켜줍니다. 7번 꼭짓점을 파란색으로 칠하고 나면 모든 꼭짓점이 색칠되므로, 모든 꼭짓점을 굵은 원으로 표시해줍니다.

이렇게 꼭짓점을 색칠해나가는 과정에서 같은 색으로 칠한 이웃한 꼭짓점이 발견될 경우 Reject하는 알고리즘을 짜면 2-coloring 문제를 해결하는 알고리즘을 만들 수 있습니다.

이 알고리즘은 모든 꼭짓점을 차례대로 방문합니다. 그리고 각 방문에서, 방문한 꼭짓점과 연결된 모든 꼭짓점을 체크합니다. 따라서 이 알고리즘의 Running Time은 $O\left( n^2 \right)$입니다. 따라서, $2Color \in \textbf{P} $라고 할 수 있겠죠.

 

Complexity Class NP

이제 위의 확장판이라고 할 수 있는 k-Coloring 문제를 보겠습니다. 규칙은 완벽히 같지만, 사용 가능한 색의 개수를 $k$개로 늘린 것입니다. 아래는 3-Colorable Graph의 예시입니다.

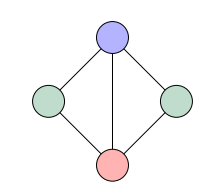
$k=2$일 경우 $kColor \in \textbf{P} $라는 것을 방금 확인했습니다. 그러나 $k$가 3 이상일 경우 $kColor$가 $ \textbf{P} $의 원소인지 아닌지는 아직 증명된 바가 없습니다. 다시 말해, 어떤 그래프가 주어졌을 때 이 그래프가 k-Colorable인지 아닌지를 Polynomial Time에 밝혀낼 수 있는 알고리즘이 존재할지 하지 않을지 모릅니다.

 

이렇게 한 그래프에서 모든 꼭짓점을 지나면서 마지막에 다시 시작 지점으로 돌아오는 Path를 Hamilton Cycle이라고 합니다. Hamilton Cycle이 존재하는 그래프의 이진 표현의 집합을 $HC$라고 하면, 이 $HC$ 역시 $ \textbf{P} $의 원소인지 아닌지는 아직 증명된 바가 없습니다.

 

Sum of Subset이라는 언어를 아래와 같이 정의하겠습니다.

$$SOS=\left\{\left<a_1, a_2, a_3, \cdots, a_n, b \right> \right\}$$

이 때, $ a_1, a_2, a_3, \cdots, a_n $ 중 몇개를 선택하여 더해 $b$를 만들 수 있어야 합니다. 예를 들어 1, 2, 7, 8, 16, 11은 $SOS$의 원소입니다. $1+2+8=11$이기 때문이죠. 그러나 1, 2, 7, 8, 16, 12는 $SOS$의 원소가 아닙니다. 1, 2, 7, 8, 16 중 일부를 선택하여 더해 12를 만들 수 없기 때문입니다.

이렇게 만들어진 언어 $SOS$ 역시 $ \textbf{P} $의 원소인지 아닌지 증명된 바가 없습니다. 다시 말해 어떤 수열이 주어졌을 때 Polynomial Time 안에 이 수열이 위 조건을 만족하는지 하지않는지 밝혀낼 수 있는 알고리즘이 존재할지 하지 않을지 모릅니다.

 

다른 예시를 한번 보겠습니다. 2 이상의 정수 중 소수가 아닌 수를 이진법으로 나타낸 문자열을 나타내는 언어를 $NPrim$이라고 하겠습니다. 이 언어는 $ \textbf{P} $의 원소일까요? 그렇습니다. 이는 비교적 최근인 2002년에 증명되었습니다. 

 

여기서 $kColor$, $HC$, $SOS$, $NPrim$과 같은 집합이 공통적으로 가지는 특징이 있습니다. 어떤 문자열이 이 집합에 포함되는지, 포함되지 않는지를 Polynomial Time에 밝혀내는 것은 쉽지 않습니다. (3개는 가능한지조차 모르고, $NPrim$ 역시 최근에 $ \textbf{P} $임이 증명되었죠.) 그러나 누군가 주어진 문자열에 대한 힌트를 제공줬을 때, 그 힌트를 통해 문자열이 집합에 포함되는지 포함되지 않는지 밝혀내는 것은 쉽다는 것입니다.

예를 들어 1, 2, 7, 8, 16, 11이라는 문자열이 $SOS$의 원소인지 아닌지를 Polynomial Time에 밝혀내는 알고리즘이 존재하는지, 하지 않는지 저희는 아직 알지 못합니다. 그러나 누군가 1, 2, 8이라는 힌트를 말해주면 이 세 숫자의 합이 11이 된다는 것은 Polynomial Time에 증명할 수 있죠.

예시로 $NPrim$도 한번 보겠습니다. $NPrim$이 $ \textbf{P} $에 속한다는 사실은 비교적 최근에 증명되었다고 했잖아요? 이건 어떤 2 이상의 정수가 합성수인지 아닌지를 Polynomial Time에 밝혀내는 알고리즘이 여기서 다룰 만큼 쉽지 않다는 것을 의미합니다. 그러나 만약 우리가 힌트를 제공받을 수 있다면, 증명은 매우 단순해집니다.

2 이상의 정수 $x$가 $NPrim$에 속하는지 아닌지를 판단하려고 하는데, 힌트로 $x$는 $a$와 $b$의 곱이라는 사실이 주어졌다고 가정합시다. 그러면 이 힌트가 진짜 정답인지를 확인하기 위해 저희가 증명해야 할 것은 총 3가지입니다.

• $ 2\leq a<x$
• $ 2\leq b<x$
• $x=ab$

그리고 정말 당연하게도 이 3가지는 Polynomial Time에 증명할 수 있습니다.

이렇게 Polynomial Time에 정답을 얻기는 힘들지만, 어떤 힌트가 정답임을 Polynomial Time 내에 증명할 수 있는 $kColor$, $HC$, $SOS$, $NPrim$과 같은 집합들을 $ \textbf{NP} $ 라고 부릅니다.

수학적인 표현으로, 모든 문자열 $w$에 대해 아래 조건을 만족하는 다항식 $p$와 언어 $B\in \textbf{NP}$가 존재할 때, 언어 $A$를 $\textbf{NP}$에 속한다고 합니다.

$$ w\in A \Leftrightarrow \exists s : \left|s \right| \leq p\left ( \left|w \right| \right )\wedge \left<w, s \right>\in B $$

여기서 언어 $B$는 문자열 $w$에 대한 옳은 정답을 $s$라고 했을 때 $ \left<w, s \right> $의 집합이며, Verification Language라고 부릅니다. 이 Verification Language가 Polynomial Time인 언어를 우리는 $\textbf{NP}$ 에 속한다고 하는 것이고요.

 

이 글에서는 어떤 문제를 얼마나 빠르게 해결할 수 있는가를 판단하는 기준과, 이를 통해 어떤 문제가 $\textbf{P}$ 와 $\textbf{NP}$ 에 속하는지 판단하는 과정을 살펴보았습니다.

감사합니다.

---

이 글은 컴퓨터공학과 학부생이 개인 공부 목적으로 작성한 글이므로, 부정확하거나 틀린 내용이 있을 수 있으니 참고용으로만 봐주시면 좋겠습니다. 레퍼런스 및 글에 대한 기본적인 정보는 이 글을 참고해 주세요.